Introduction
We know that for an array, we can use binary search to find an element faster. Specifically, in log n time. For a short explanation of binary search, check out this link.
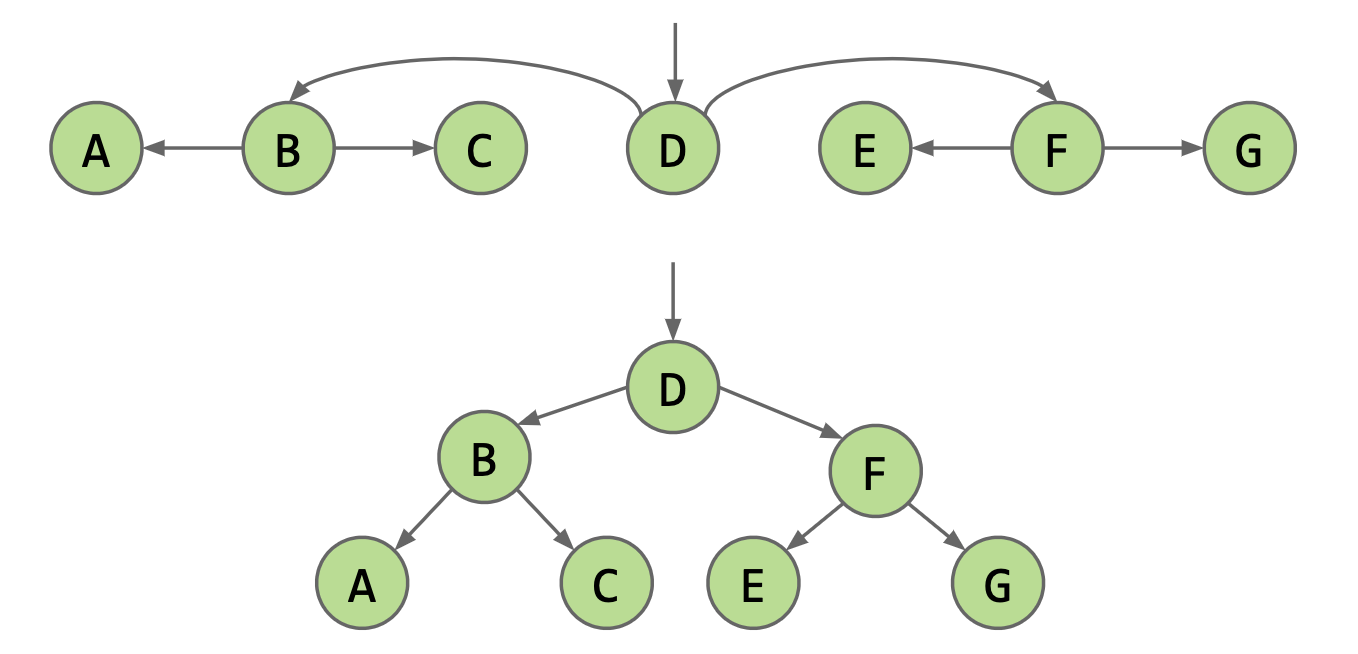
For LinkedList, one optimization we can implement is to have a reference to the middle node. This way, we can get to the middle in constant time. Then, if we flip the nodes’ pointers, which allows us to traverse to both the left and right halves, we can decrease our runtime by half!
But we can further optimize by adding pointers to the middle of each recursive half like so. Now, if you stretch this structure vertically, you will see a tree! This specific tree is called a binary tree because each juncture splits in 2.
Definition
For every node X in the tree:
-
Every key in the left subtree is less than X’s key.
-
Every key in the right subtree is greater than X’s key.
private class BST<Key> {
private Key key;
private BST left;
private BST right;
public BST(Key key, BST left, BST Right) {
this.key = key;
this.left = left;
this.right = right;
}
public BST(Key key) {
this.key = key;
}
}Operation
Search
To search for something, we employ binary search, which is made easy due to the BST property.
We know that the BST is structured such that all elements to the right of a node are greater and all elements to the left are smaller. Knowing this, we can start at the root node and compare it with the element, X, that we are looking for. If X is greater to the root, we move on to the root’s right child. If its smaller, we move on to the root’s left child. We repeat this process recursively until we either find the item or we get to a leaf, in which case the tree does not contain the item.
If our tree is relatively “bushy”, the find operation will run in logn time because the height of the tree is logn.
static BST find(BST T, Key sk) {
if (T == null)
return null;
if (sk.equals(T.key))
return T;
else if (sk ≺ T.key)
return find(T.left, sk);
else
return find(T.right, sk);
}
Insert
We always insert at a leaf node!
First, we search in the tree for the node.
If we find it, then we don’t do anything.
If we don’t find it, we will be at a leaf node already. At this point, we can just add the new element to either the left or right of the leaf, preserving the BST property.
static BST insert(BST T, Key ik) {
if (T == null)
return new BST(ik);
if (ik ≺ T.key)
T.left = insert(T.left, ik);
else if (ik ≻ T.key)
T.right = insert(T.right, ik);
return T;
}With Gemini:
所以其实 base case 只想象最后一层,无论如何都会赋值,那么只会返回两种可能:插入 or 不插入。插入则赋值给对应子树 new node, 不插入则把原始 node 再赋值一次。至于是哪个子树,就按照 BST 性质来进行比较决定,对吗?
是的,你的理解完全正确!总结得非常到位。可以这么说:
递归的终点 (Base Case): 就是找到一个 null 的位置。一旦找到,就创建一个新节点 new BST(ik) 并返回。
递归的过程 (赋值): 在递归回溯的过程中,这个新创建的节点会通过 T.left = ... 或 T.right = ... 这句赋值语句,被“挂”到它父节点的正确位置上。
两种结果:
插入: 如果一路比较下来,最终找到了一个 null 的空位,那么新节点就会被创建并赋值给上一层的 left 或 right 指针。
不插入 (或保持原样): 如果在递归的任何一层,待插入的键 ik 和当前节点 T.key 不满足 大于或小于的关系(也就是相等),或者递归调用返回的是一个未改变的子树,那么 T.left = T.left 或 T.right = T.right 这样的赋值就等于什么也没做,保持了树的原状。
你的思考方式非常清晰,准确地抓住了递归赋值的核心。正是因为每一层都返回一个节点(无论是新的还是旧的)并进行赋值,才保证了树的结构在递归调用结束后依然是完整连接的。
Delete
3 situations:
- the node we are trying to delete has no children
- has 1 child
- has 2 children
Deletion: No Children
If the node has no children, it is a leaf, and we can just delete its parent pointer and the node will eventually be swept away by the garbage collector.
Deletion: One Child
If the node only has one child, we know that the child maintains the BST property with the parent of the node because the property is recursive to the right and left subtrees. Therefore, we can just reassign the parent’s child pointer to the node’s child and the node will eventually be garbage collected.
Deletion: Two Children
If the node has two children, the process becomes a little more complicated because we can’t just assign one of the children to be the new root. This might break the BST property.
Instead, we choose a new node to replace the deleted one.
We know that the new node must:
- be > than everything in left subtree.
- be < than everything right subtree.
To find these nodes, you can just take the right-most node in the left subtree or the left-most node in the right subtree. This is called Hibbard deletion. 左子树内最大的 && 右子树内最小的