Introduction
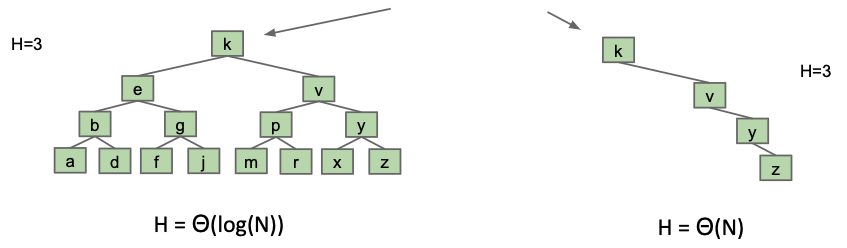
我们插入节点的顺序对 BST - Binary Search Tree 的高度和平均深度有重大影响。
在插入顺序不美妙时,可能在同等树高下存储的元素变少,而平均树高和深度恰恰和 BST 的表现有相关性。As such, we need a different way to maintain “bushiness” in our search trees. 茂密
To solve this problem, we introduce to B Tree, a kind of self-balancing search tree. B-Trees are a modification of the BST.
Iteration
Avoiding Imbalance
鉴于插入新节点可能导致不平衡,故而直接选择不插入新节点,而是使 leaf node 可以容纳多个值,当 insert search 到 leaf node 的时候(找到了应该的问题),就将此值插入 leaf node.
Instead of adding a new node upon insertion, we simply stack the new value into an existing leaf node at the appropriate location. However, a clear problem with this approach is that it results in large leaf nodes that basically become a list of values, going back to the problem of linear search.
为了规避在某些 leaf 上存在海量值让 search 变成 O(n),则需要试图引入一种能让 tree 自动生长的机制,like if values contain in leaf > 4, do something to make it always < than 4.
Moving Items Up
A B-Tree has a limit L on the number of values a node can hold, instead of having one item per node like a BST. To ameliorate the issue of overly stuffed leaf nodes, we may consider “moving up” a value when a leaf node reaches a certain number of values.
下图第一组展示了 L=3(每个 node 内的值不能超过三个)时,将 25、26 add 后,右下角 node 超载而提升的过程。提升会选择左侧第二个 21,然后将 21 的左右分裂成两个单独的 node。
提升后上层超载,则继续选择左侧第二个 17 提升,小于 17 的划归给 17 分裂出的左子树,大于 17 的划归给右子树。如此操作后依旧平衡。
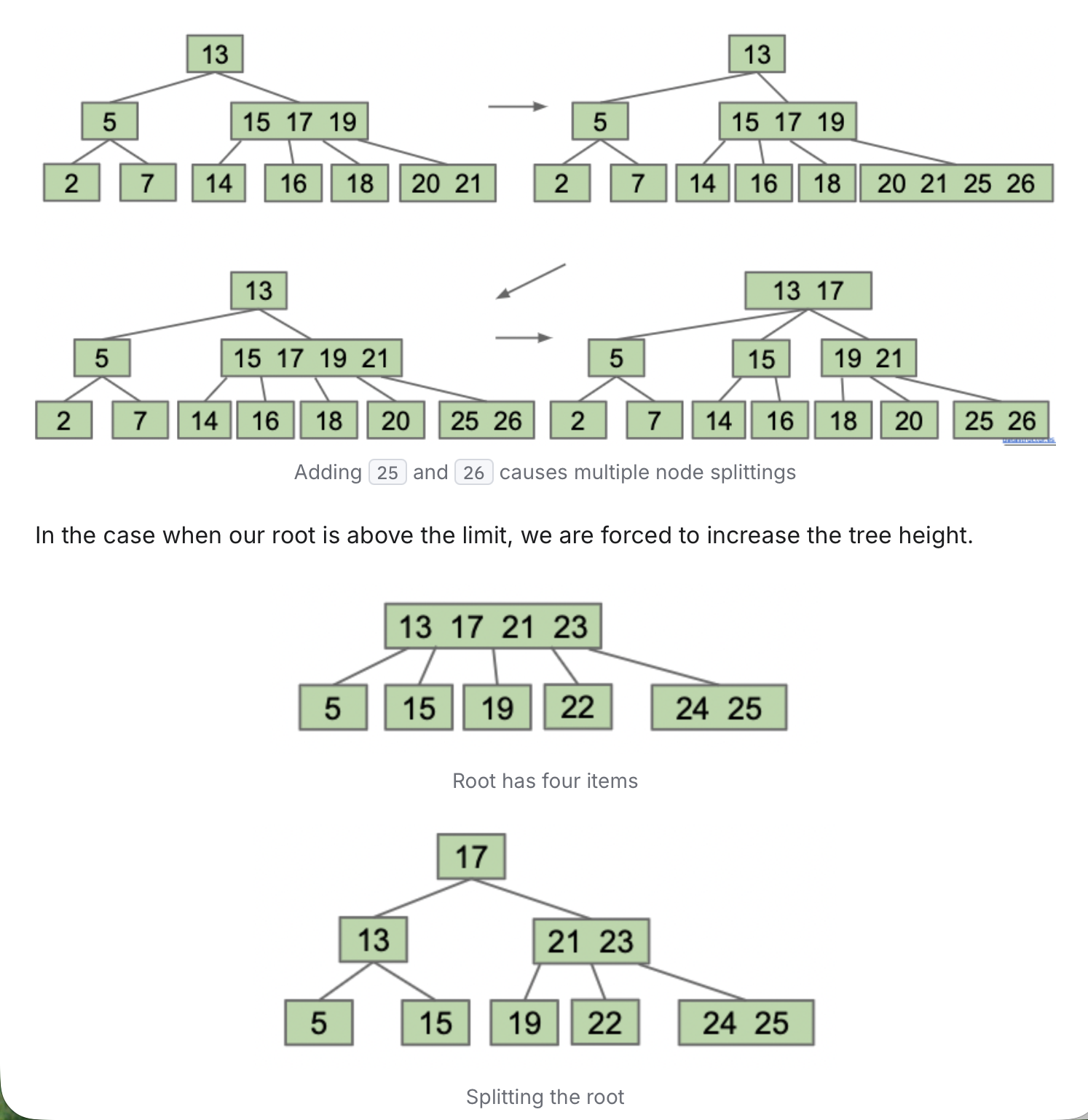
上图下半部分展示了根节点超载如何处理。同上,依旧是选择左侧第二个提升,划分左右子树,小于左侧第二个的归左子树,大于的归右子树。
Definition
If we split the root, every node is pushed down by one level.
If we split a leaf or internal node, the height does not change. There is never a change that results in imbalance.
The real name for this data structure is a B-Tree.
B-Trees with a limit of 3 items per node are also called 2-3-4 trees or 2-4 trees (a node can have 2, 3, or 4 children). Setting a limit of 2 items per node results in a 2-3 tree (a node can have 2, or 3 children).
最大 value 数量 = 最大子节点数量 - 1
Because of the way B-Trees are constructed, they have two invariants:
-
All leaves are the same distance from the root.
-
A non-leaf node with k items must have exactly k + 1 children.
These two invariants guarantee a “bushy” tree with logN height.
Usage
B-Trees are used mostly in two specific contexts:
first, with a small L for conceptually balancing search trees, or secondly, with L in the thousands for databases and filesystems with large records.